Princip univerzalonosti

Princip univerzalnosti

Poslednjih godina mi je žao što sem kao većina lekara, izbegavao matematiku. Iako mi je čudno izgledala priča o teoriji svega, magičnoj formuli koja izražava sva dešavanja u Svemiru, poslednjih godina matematika je ukazala na neke univerzalne principe. Češki matematičar Petr Šeba je jednog dana 1999 sedeo u Meksiku i posmatrao vozače autobusa umestu Cuernavaca, u Meksiku. Primetio je mladiće koji su vozačima dodavali papiriće, za koje sui m oni davali novac. Saznao je da vozači plaćaju mladiće da ih obaveštavaju o vremenu polaska prethodnog autobusa. Ako je prethodni prošao skoro, vozač je vozio sporo, da bi se do dolaska na sledeću stanicu skupilo više putnika., Ako je bio davno, vozač je išao brže, da stigne pre onog iza. Ovo mu je izgledalo slično fenomenu koji se u kvantnoj fizici opisuje kao kvantni sistemi haosa. Uedio je mladiće da mu daju ceduljice nekoliko dana, a kada je podatke ubacio u kompjuter dobio je rezultate koji su se poklapali sa rezultatima ekspreimenta u kvantnoj fizici.

U kasnijim godinama, sličan matematički obrazac je otkriven u brojnim drugim sistemima. Ova pojava se naziva fenomenom univerzalosti i može da objasni promene klime na Zemlji  ili programe na Intenetu.  U svakom spektru, iako su podaci slučajno rasporedjeni, vidi se isti obrazac. Posle dve bliske linije (dogadjaja), dolazi do nastajanja razmaka. Ovaj fenomen se može izraziti jednostavnom matematičkom formulom. Možemo predvideti ponašanje sledeće linije (dogadjaja), ako poznajemo formula po kojoj se organizuju.

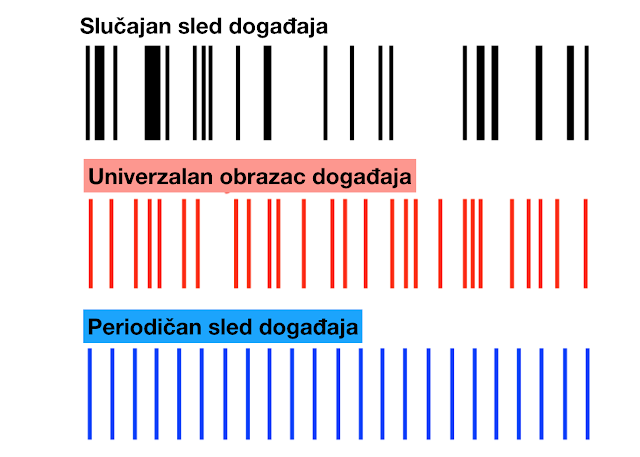
Slika 1. Na gornjoj slici je prikaz slučajnih događaja, a na sasvim donjoj periodičnih. Međutim, u složenim sistemima, iz nama nejasnih razloga, nastaje univerzalan obrazac (u komse posle dva bliska događaja, sledeći javlja kasnije, a posle dva udaljena sledeći ranije=.

Zašto se kompleksni sistemi ponašaju na ovaj način nije poznato.  Ipak, kako kaže Van Vu, matematičar sa Jejla, “liči da se radi o prirodnom zakonu”. Od kristalne rešetke vode do strukture interneta, postoji predvidljiv način ponašanja elemanata u kompleksnoj matrici sistema. Zanimljivo, što je system kompleksniji, to je obrazac čvršći i predvidljiviji.  To je kao ponašanje velikog broja ljudi u istoj prostoriji, ukoliko nešto zajedno rade, ličnost pojedinca nije od velikog značaja. U malim grupama, pojedinac I njegova uloga su znatno izraženiji.

Teško je definisati slučajnost, ali se ona podvrgava principima simetrije i univerzalnosti. Simetrija označava da ukoliko se neki dogašaj ponovi mnogo puta, ishod će biti skoro uvek fifti/fifti (kao kada bacate novčlć desetak minuta, na kraju je rezultat da li će pasti na jednu ili drugu stranu isti ili skoro isti). Univerzalost govori da ukoliko je ishod nekog događaja posledica različitih izvora slučanosti, detalji mehanizma kojim se on dogodio nisu važni (tri puta sam čitao ovu rečenicu). Na primer, ponašanje svih tečnosti se može opisati jednom, jednostavnom formulom. Još 1827 Škotski botaničar Robert Brown je posmatrajući polenova zrna pod mikroskopom, uočio njihovo haotično kretanje u tečnosti (koje je po njemu dobilo ime Braunovo kretanje). Fenomen su objasnili 1905. godine nezavisno Albert Einstein i Marian Smoluchowski: molekuli u tečnosti vibriraju, udarajući mikroskopske čestice. Ovo stvara nasumično kretanje.  Iako je kretanje sasvim slučajno, može se izračunati verovatnoća kretanja pojedinačne čestice. Ponašanje čestica se može opisati istom formulom koja objašanjava kretanje toplote kroz tela, Joseph Fourierovom toplotnom jednačinom. Braunovo kretanje je univerzalno. Francuski matematičar Louis Bachelier je zapazio isti obrazac kada je proučavao finansijski sistem. Sa velikom verovatnoćom se može izračunati kretanje akcija na berzi na osnovu pomenute formule. Ponašanje atoma se opisuje istim formulama.  Nije nam jasno zašto se obrazac slučajno-ali ipak pravilno javlja u kompleksnim sistemima. Ipak, jasno je da se Svemir pokorava zakonima matematike.

Proučavanje plazme na ekstremno visokim temperaturama ili gasa na apsolutnoj nuli, ukazuju na isti princip univerzalnosti. Složeni sistem se ponaša kao fraktalni (pisao sam o fraktalima u ranije postu), skoro identično u različitim prostorno/vremenskim uslovima. Ponašanje se ponekad može opisati kao umnožak veoma jednostavnih brojeva, kao što su 12 ili −13. Još 1941. Je ruski matematičar Andrej Kolmogorov opisao kako se  ponaša kafa, kada je mešate da se brže ohladi. On je pokazao da veliki vrtlog tečnosti stvara manje vrtloge, a ovi još manje itd. Smanjenje energetskog nivoa se odigrava u stepenicama od −53. Ovo fraktalno ponašanje materije mi znamo intuitivno, kada želite da neka tečnost bude ravnomerno zaslađena, mešate je.

Da li se život može opisati matematičkim modelom? Iako to ne izgleda moguće na prvi pogled, setimo se da smo načinjeni od atoma, koji se pokoravaju prinipcu univerzalnosti. Svaki elektron u našeom telu ima iste matematičke osobine, -1, ½ i 1! Nemamo druga svojstva, osim onih koji se mogu opisati matematički. Uzmimo na primer izračunavanje brzine metabolizma, koje se ponaša kao prethodno opisan princip hlađenja kafe. Za svako udvostručvanje mase organizma, metaboličke potrebe rastu za ¾ (ovo važi za 27 redova veličine, od bakterije do slona).Slična skala se može primeniti na dužinu života, brzinu rasta, dužinu DNK, visinu drveća ili masu mozga. Sve ove osobine se menjaju kao umnožak ¼ (ovo se naziva “alomerička skala jedne čevrtine”). Na primer, brzina disanja se izražava kao površina tela pomnožena sa ¼. Iako je svaki organizam nastao i razvijao se u savim drugačijim uslovima, sa drugačijom genetikom njihov razvoj se podvrgava jednostavnom matematičkom modelu. Da li nam ovo ukazuje da možemo da dođemo matematički do pojma svesti, koji nam za sada izmiče empirijskim isptraživanjima? Da li nas matematički model može odvesti do Tvorca? Čeka nas uzbudljiv period.